Analisi Matematica II: Le curve – Pt. 1 – Teoria

In questo primo video del corso (pratico) di Analisi Matematica II si trattano le curve e in particolar modo tutti gli aspetti fondamentali per la risoluzione degli esercizi.
Si definiscono le curve e le loro proprietà (chiusura, semplicità, regolarità e lunghezza). Viene trattata la differenza tra curva, grafico di una curva e sostegno di una curva.
Viene mostrato un significato fisico della curva: essa viene vista come la legge oraria di un punto materiale cosicché il sostegno della curva diventi la traiettoria descritta dal punto e derivata prima e seconda diventino velocità e accelerazione istantanee del punto.
Analisi Matematica II: le curve – Esercizio 1

Nel video vengono studiate la chiusura, la semplicità e la regolarità di una curva assegnata.
L’esercizio viene svolto utilizzando le formule mostrate nel video della prima parte di teoria.
Analisi Matematica II: le curve – Esercizio 2

Nel video vengono studiate la chiusura, la semplicità e la regolarità di una curva assegnata.
Viene inoltre calcolata la lunghezza della curva e mostrata l’analogia esistente tra il sostegno della curva e la traiettoria di un punto materiale che si muove secondo la legge della curva. L’esercizio viene svolto utilizzando le formule mostrate nel video della prima parte di teoria.
Analisi Matematica II: le curve – Esercizio 4

Nel video vengono studiate la chiusura, la semplicità e la regolarità di una curva assegnata. Ne viene, inoltre, calcolata la lunghezza. L’esercizio viene svolto utilizzando le formule mostrate nel video della prima parte di teoria.
Analisi Matematica II: le curve – Esercizio 5

Nel video vengono determinati la curvatura e il raggio di curvatura di una curva in un dato punto del suo sostegno. Conoscendo il punto del sostegno viene ricavato il rispettivo valore di “t”. Viene anche calcolato il centro della circonferenza osculatrice. L’esercizio viene svolto utilizzando le formule mostrate nel video della prima parte di teoria.
Analisi Matematica II: Campi vettoriali – Lezione 1 – Teoria

Nel video vengono spiegati (in modo informale) concetti teorici necessari per la risoluzione degli esercizi sui campi vettoriali.
In particolare modo, vengono trattati i seguenti temi:
– la definizione di un campo vettoriale
– la connessione semplice degli insiemi
– l’irrotazionalità di un campo vettoriale
– la conservatività di un campo vettoriale e la sua funzione potenziale
– il lavoro svolto da un campo vettoriale lungo una curva
Analisi Matematica II: Campi vettoriali – Lezione 2 – Esercizio 1

Nel video viene studiato un campo vettoriale in R². In particolare, vengono determinati: – il dominio del campo vettoriale – l’irrotazionalità e la conservatività del campo vettoriale – il lavoro lungo una curva chiusa – il lavoro lungo una curva aperta – una curva tale che il lavoro del campo vettoriale lungo di essa valga 3.
Analisi Matematica II: Campi vettoriali – Lezione 3 – Esercizio

Nel video viene risolto un esercizio in cui dato un campo vettoriale se ne verifica la conservatività e se ne calcola il potenziale che vale 4 nel punto (1,0).
Analisi Matematica II – Campi vettoriali – Lezione 4 – Esercizio

Studio di una forma differenziale: calcolo delle primitive (dopo averne verificate l’esattezza) e dell’integrale lungo una curva.
Analisi Matematica II: Campi vettoriali – Lezione 5 – Dimostrazione

Nel video viene dimostrato che per un campo vettoriale conservativo l’integrale curvilineo di II specie può essere calcolato dome differenza di potenziale tra il punto finale e il punto iniziale della curva.
Analisi Matematica II: Campi vettoriali – Lezione 6 – Dimostrazione

In tale video viene dimostrato che se gli integrali curvilinei di II specie di un campo vettoriale lungo due curve aventi estremi coincidenti sono uguali allora l’integrale del campo vettoriale lungo una curva chiusa vale 0. Vale anche l’implicazione inversa.
Analisi Matematica II: Funzioni di due variabili – Lezione 1 – Dominio e Limiti
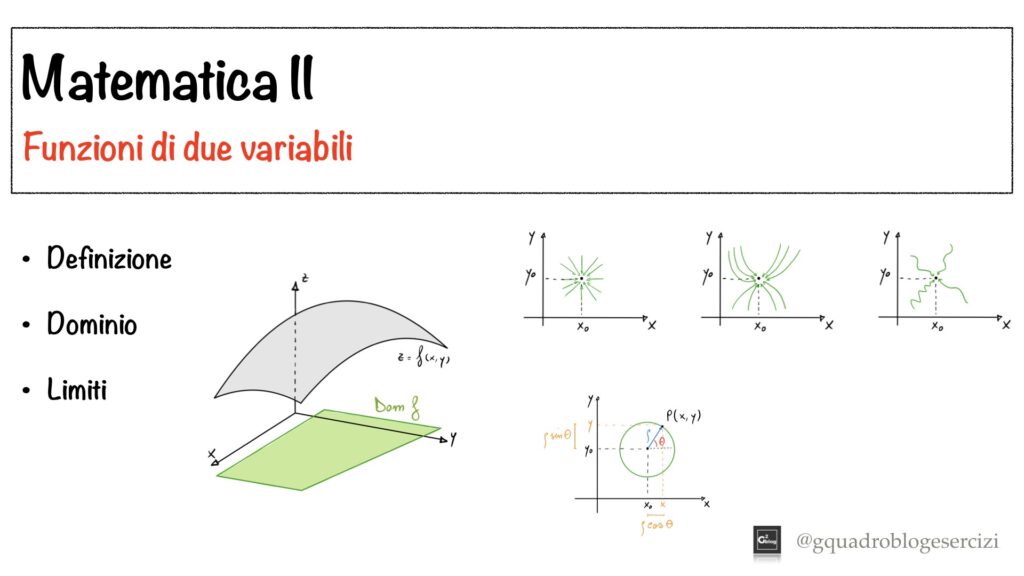
Nel video si introducono in modo informale le funzioni di due variabili e se ne calcolano il dominio e i limiti.
Analisi Matematica II: Insiemi – Lezione 1 – Definizioni ed esempi
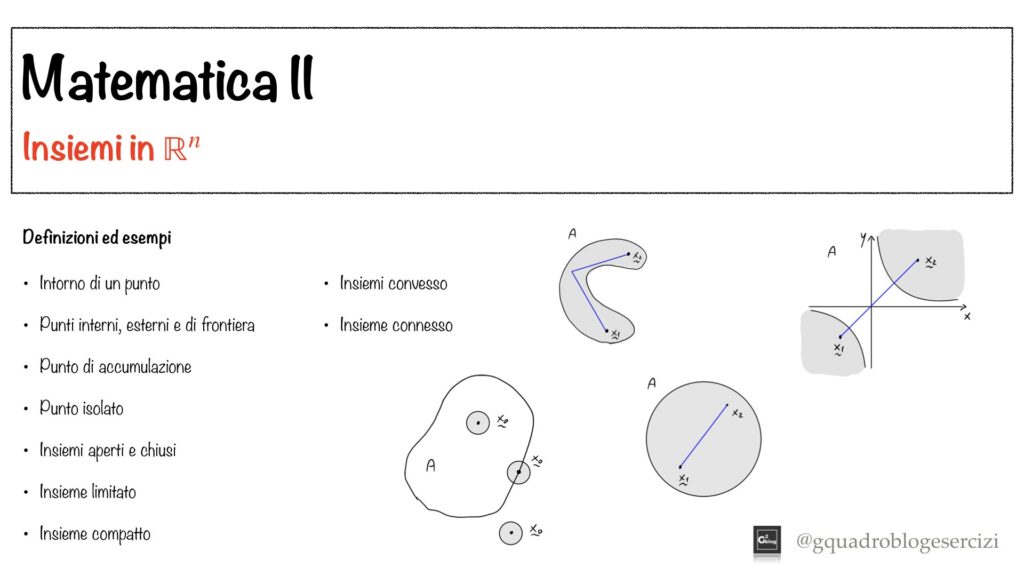
Nel video si forniscono definizioni ed esempi dei seguenti concetti:
– Intorno di un punto
– Punti interni, esterni e di frontiera
– Punto di accumulazione
– Punto isolato
– Insiemi aperti e chiusi
– Insieme limitato
– Insieme compatto
– Insiemi convesso
– Insieme connesso
Analisi Matematica II: Funzioni di due variabili – Lezione 2
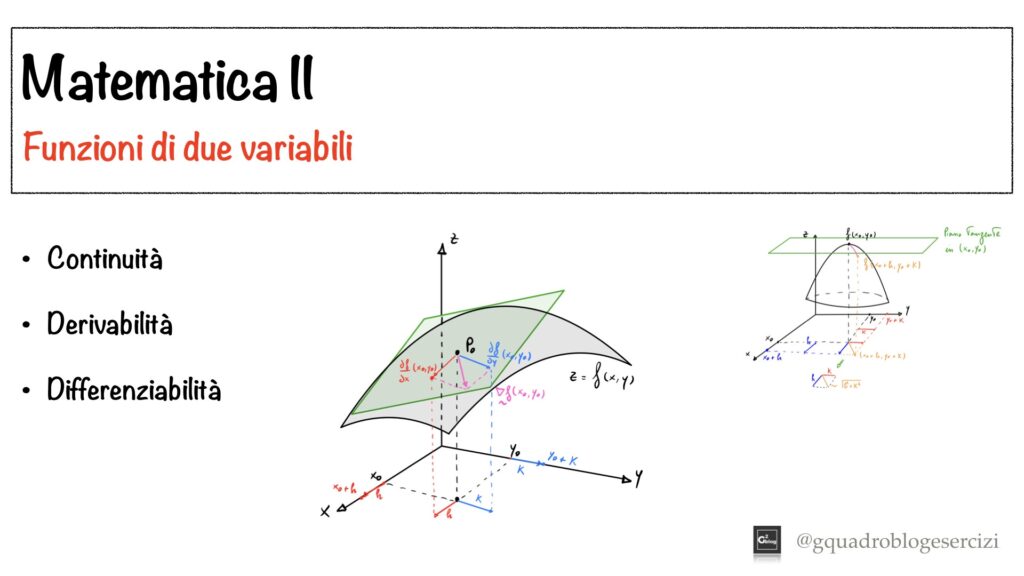
Nel seguente video vengono spiegati, con relativi esempi, i seguenti concetti relativi a funzioni di due variabili: – Continuità in un punto – Derivabilità in un punto – Derivata direzionale – Differenziabilità. Per ognuno viene spiegato anche il significato fenomenologico (o geometrico).
Analisi Matematica II: Funzioni di due variabili – Lezione 3 – Esercizi

Nel video vengono svolti due esercizi in cui date due funzioni bisogna determinarne il dominio e il piano tangente in un punto.
Analisi Matematica II: Funzioni di due variabili – Lezione 4 – Esercizio

Nel video viene svolto un esercizio in cui data una funzione bisogna determinarne il dominio, il piano tangente in un punto e la derivata direzionale lungo la direzione di una bisettrice.
Analisi Matematica II: Funzioni di due variabili – Lezione 5 – Esercizio

Nel video viene svolto un esercizio in cui data una funzione bisogna determinarne il dominio, il piano tangente in un punto e la derivata direzionale lungo la direzione di una bisettrice.
Analisi Matematica II: Funzioni di due variabili – Lezione 6 – Esercizio

Nel video viene svolto un esercizio in cui data una funzione bisogna determinarne la Differenziabilità in un punto. Vengono quindi verificate anche la continuità e la Derivabilità della funzione nello stesso punto facendo uso dei limiti.
Analisi Matematica II: Funzioni di due variabili – Lezione 7 – Dimostrazioni

Nel video vengono dimostrate due proposizioni inerenti alle funzioni di due variabili: la prima asserisce che se una funzione è differenziabili in un punto allora la funzione è ivi continua; la seconda che se la funzione è differenziabile in un punto allora in quel punto esistono le derivate direzionali e possono essere calcolate come il prodotto scalare tra il vettore gradiente e il vettore direzione
Analisi Matematica II: Funzioni di due variabili – Lezione 8 – Dimostrazione

Nel video viene dimostrato il teorema del differenziale totale: se una funziona presenta in un punto derivate continue allora in quel punto la funzione è differenziabile.
Analisi Matematica II: Estremi locali e globali – Lezione 1
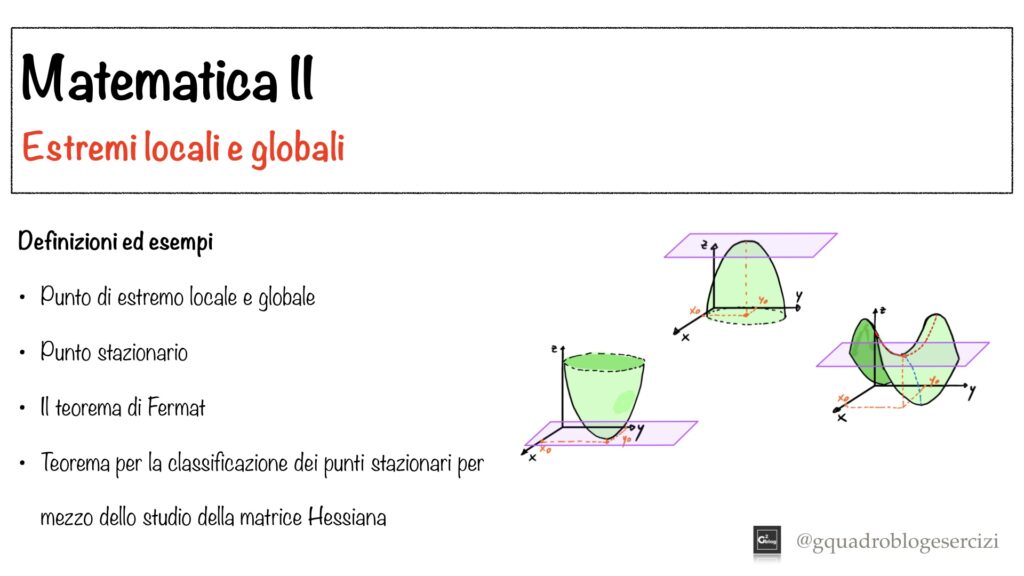
Nel video vengono spiegati i seguenti concetti:
– Punto di estremo locale e globale per una funzione
– Punto stazionario per una funzione
– I teorema di Fermat
– II teorema di Fermat (per funzioni di due variabili).
Viene, inoltre, svolto un esempio di esercizio in cui è richiesto di ricercare e classificare i punti di estremo locale di una funzione di due variabili.
Analisi Matematica II: Estremi locali e globali – Lezione 2
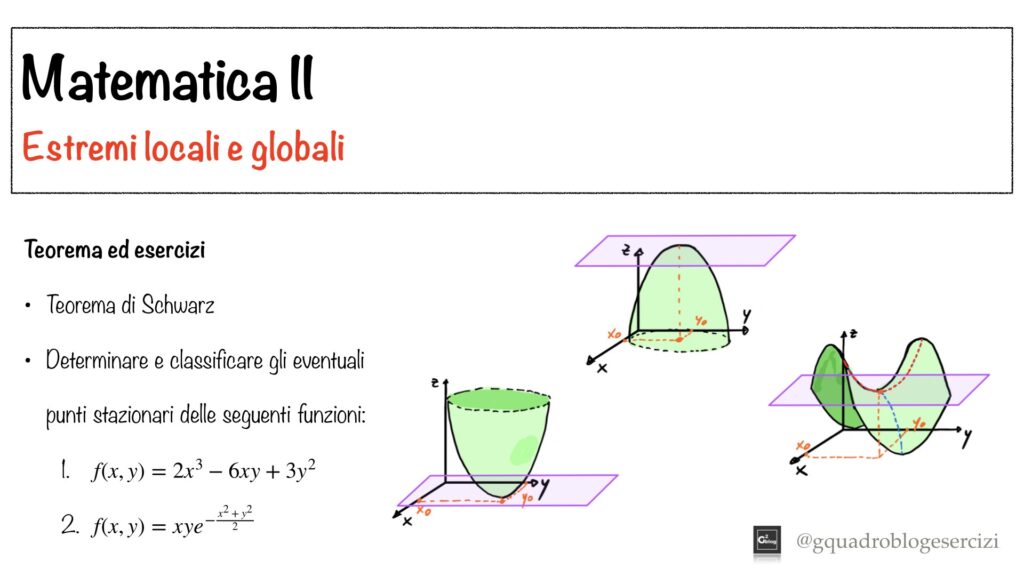
Nel video viene enunciato il teorema di Schwarz e vengono risolti due esercizi in cui si calcolano, studiandone la natura, i punti stazionari di una funzione di due variabili.
Analisi Matematica II: Estremi locali e globali – Lezione 3

Nel video vengono risolti due esercizi in cui è richiesto di calcolare i punti di massimo e minimo (locali e assoluti) di una funzione di due variabili.
Per i punti di estremo locale si utilizzano il primo e il secondo teorema di Fermat.
Per gli assoluti si studia il comportamento della funzione nel dominio.
Analisi Matematica II: Estremi locali e globali – Lezione 4

Analisi Matematica II: Estremi locali e globali – Lezione 5

Guarda il video
(Pubblicazione 20.09.2024)
In questa lezione vengono dimostrati il teorema di Fermat sui punti stazionari e il teorema che ne permette la classificazione mediante lo studio della matrice Hessiana.
Inoltre, viene rivista la differenza tra punti estremali e punti stazionari e vengono ricordate alcune proprietà delle matrici simmetriche e delle forme quadratiche (necessarie per la dimostrazione dei teoremi).
Analisi Matematica II: Massimi e minimi vincolati – Lezione 1

Nel video vengono introdotti i concetti di massimo e minimo vincolati.
In particolar modo, viene enunciato il teorema di Weierstrass e utilizzato per determinare il massimo e il minimo assoluti di una funzione su un insieme compatto.
Analisi Matematica II: Massimi e minimi vincolati – Lezione 2

Nel video vengono introdotti i concetti di massimo e minimo vincolati a funzioni della forma g(x,y)=b.
In particolar modo, viene enunciato il teorema di Lagrange e utilizzato per determinare il massimo e il minimo assoluti di una funzione sui punti di una circonferenza.
Analisi Matematica II: Massimi e minimi vincolati – Lezione 3 (Parte 1 e Parte 2)

Guarda il video Parte 1 / Parte 2
Nel video viene risolto un esercizio in cui si richiede di calcolare il massimo e il minimo assoluto di una funzione su un triangolo di vertici assegnati.
Poiché l’insieme è compatto e la funzione è continua, l’esistenza del max e min assoluti è assicurata dal teorema di Weierstrass.
Alla fine dell’esercizio viene mostrato i graficamente, tramite GeoGebra, il risultato ottenuto.
Analisi Matematica II: Equazioni Differenziali Ordinarie del I ordine – Lezione 1

Nel video vengono introdotte le equazioni differenziali ordinarie del I ordine. Vengono spiegati i metodi risolutivi per separazione di variabili e per variazione di costanti. Per ognuno viene mostrato un esempio applicativo.
Analisi Matematica II: Equazioni Differenziali Ordinarie del I ordine – Lezione 2

Nel video vengono introdotti il problema di Cauchy e il teorema di esistenza e unicità locale della sua soluzione. Vengono inoltre risoluti due esercizi per mostrare l’applicazione dei concetti teorici.
Analisi Matematica II: Equazioni Differenziali Ordinarie del I ordine – Lezione 3

Nel video vengono risolti due esercizi: un problema di Cauchy e un’equazione differenziale a variabili separabili. I risultati vengono anche graficati su GeoGebra.
Analisi Matematica II: Equazioni Differenziali di Bernoulli – Lezione 1

Guarda il video
(Pubblicazione 07.10.2024)
Nel video vengono trattate le equazioni differenziali di Bernoulli.
Dopo averne mostrato la formula generale e la procedura risolutiva, vengono risolti due esempi: nel primo si determina la soluzione di un’equazione differenziale; nel secondo si determina la soluzione di un problema di Cauchy. In quest’ultimo caso, si verifica anche che la soluzione esista e sia unica in forma locale (verificando se le funzione è lipschitziana in un intorno della soluzione).
Analisi Matematica II: Equazioni Differenziali Ordinarie del II ordine – Lezione I

Nel video viene spiegato come risolvere le equazioni differenziali ordinarie del II ordine a coefficienti costanti.
Viene mostrato come determinare la soluzione omogenea, la soluzione particolare con il metodo “ad hoc” e l’integrale generale.
Analisi Matematica II: Integrali Doppi – Lezione I – Parte 1
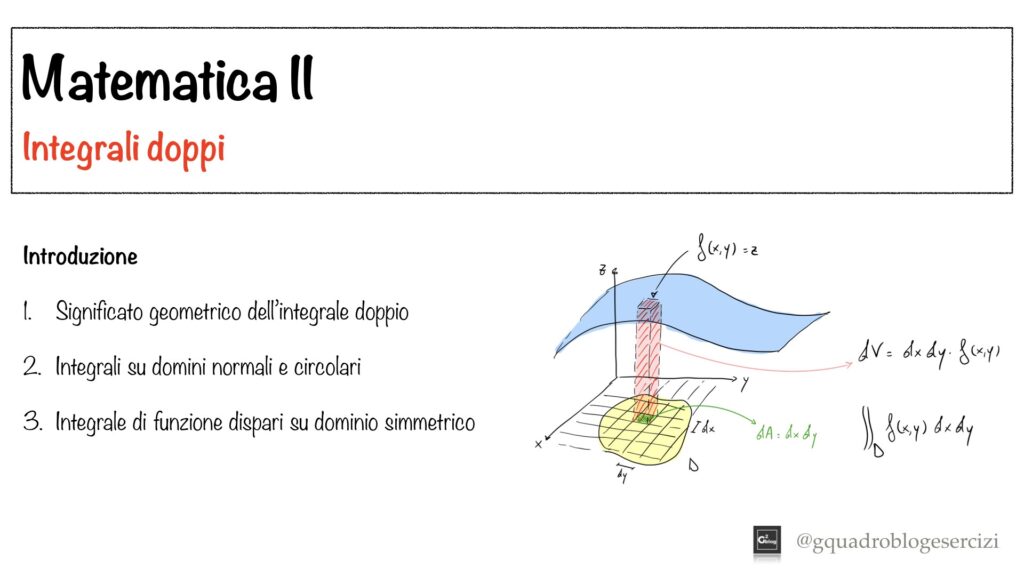
Nel video viene spiegato il significato geometrico dell’integrale doppio e come risolvere gli integrali doppi su domini rettangolari, normali rispetto a uno degli assi coordinati e circolari. Viene inoltre mostrato il valore di un integrale doppio di una funziona dispari su dominio simmetrico rispetto a uno degli assi coordinati.
Analisi Matematica II: Integrali Doppi – Lezione I – Parte 2
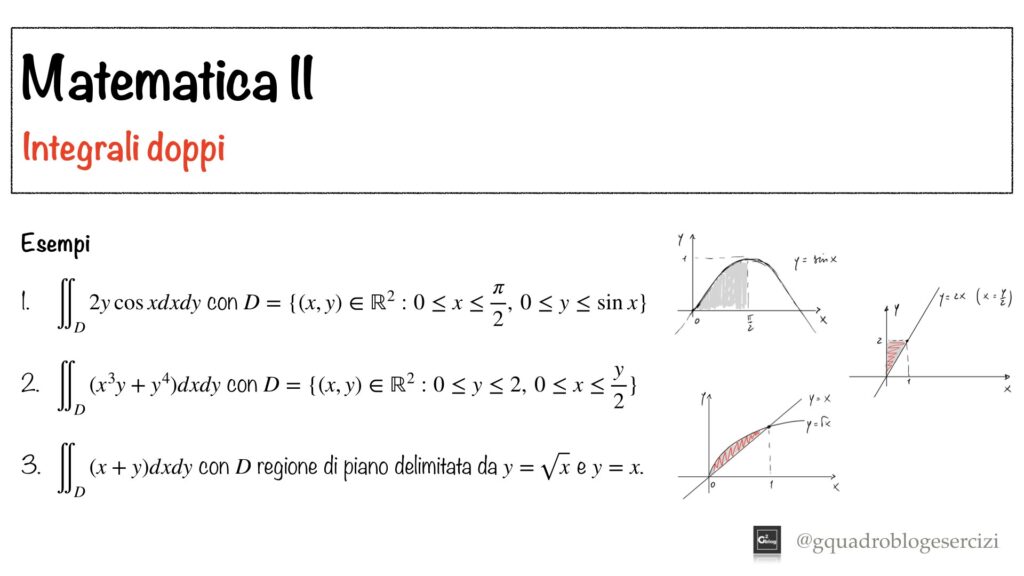
Nel video vengono risolti tre integrali doppi su domini normali rispetto a uno degli assi coordinati.
Analisi Matematica II: Integrali Doppi – Lezione 2
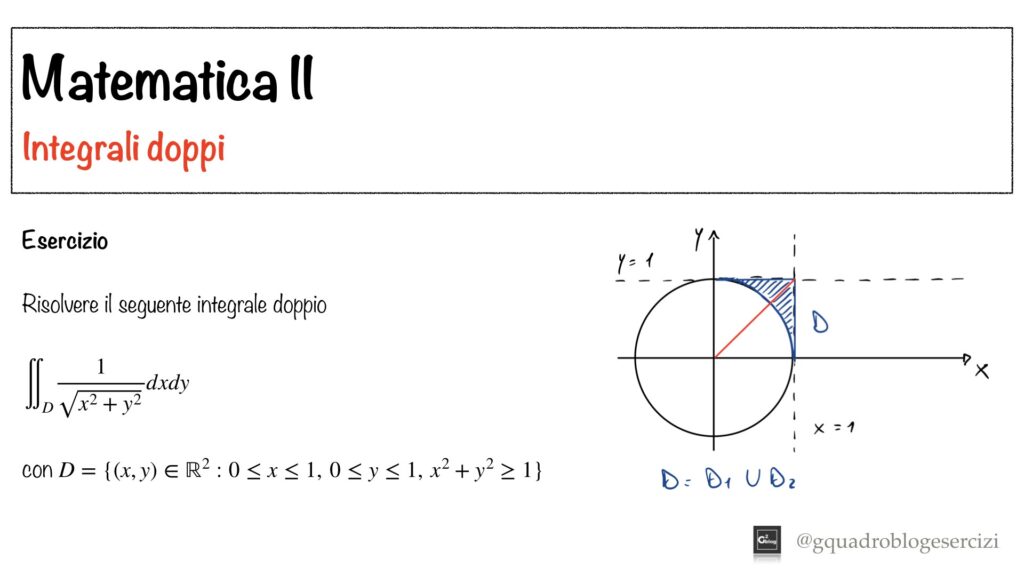
Analisi Matematica II: Integrali Doppi – Lezione 3
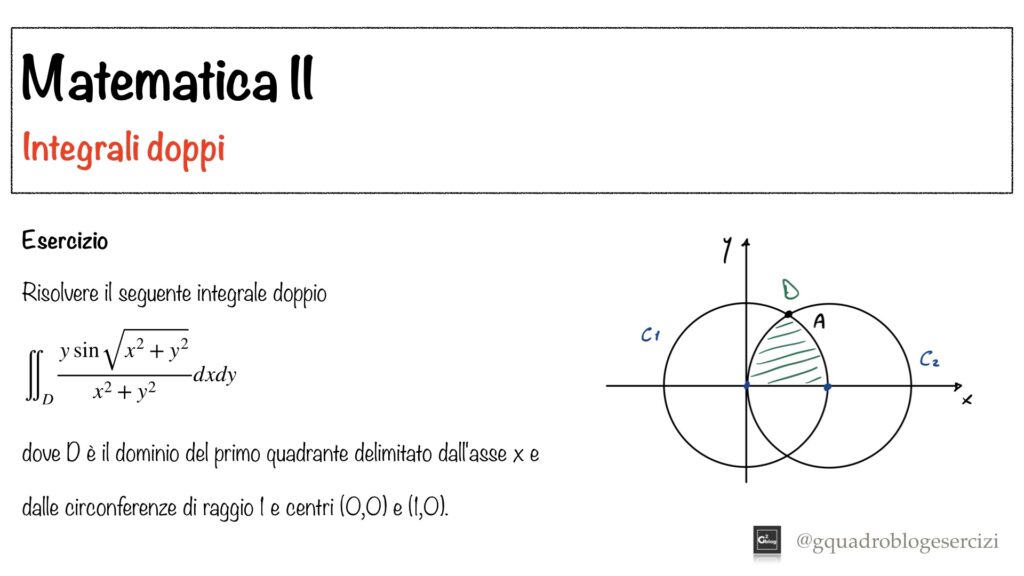
Guarda il video
(Pubblicazione 21.10.2024)
Nel video viene risolto un integrale doppio utilizzando le coordinate polari centrate nell’origine. Il dominio di integrazione viene scomposto in due risolvendo, quindi, l’integrale su ognuno di essi. Il risultato finale è dato dalla somma degli integrali.
Analisi Matematica II: Superfici – Lezione 1
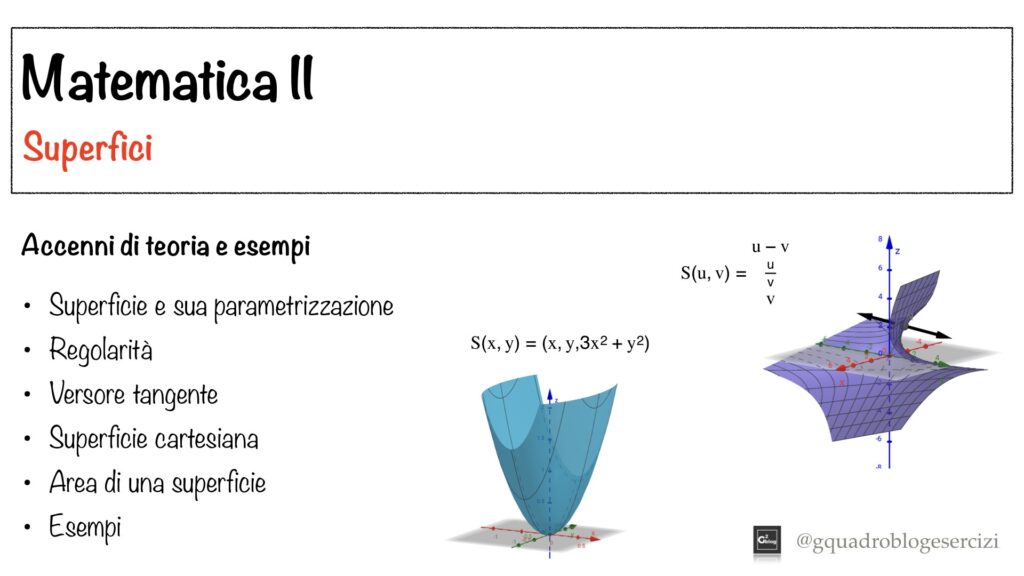
Nel video vengono trattati i seguenti concetti riguardanti le superfici:
– Superficie e sua parametrizzazione
– Regolarità
– Versore tangente
– Superficie cartesiana
– Area di una superficie
– Esempi
Analisi Matematica II: Integrali di superficie – Lezione 1

Guarda il video
(Pubblicazione 11.11.2024)
Nel video vengono trattati gli integrali di superficie. Dopo averne dato una definizione matematica e un possibile significato fisico, vengono svolti due esercizi di esempio in cui ci calcola l’integrale di una funzione di tre variabili su una superficie cartesiana. Per ognuno degli esercizi, viene anche disegnato il sostegno della superficie nello spazio cartesiano.
Analisi Matematica II: Integrali di flusso – Lezione 1

Guarda il video
(Pubblicazione 27.11.2024)
Nel video vengono trattati gli integrali di flusso. Dopo averne data la definizione matematica vengono svolti degli esempi per spiegare come determinare il verso della normale alla superficie (che determina se il flusso del campo vettoriale sia entrante o uscente) utilizzando 3 metodi: grafico, vettoriale e analitico. Infine, viene risolto un esercizio in cui si calcola il flusso di un campo vettoriale attraverso una superficie.
Analisi Matematica II: Successioni di funzioni – Lezione 1

Guarda il video
(Pubblicazione il 02/07/2024)
Nel video vengono ricapitolati alcuni concetti fondamentali riguardanti le successioni di funzioni.
Dopo aver dato la definizione di successione di funzioni, vengono trattate la convergenza puntuale e la convergenza uniforme. Viene mostrato, anche tramite esempi ( fn(x) = nxe^(-nx); fn(x) = n^2xe^(-nx) con x in [0,1]), come la convergenza uniforme consenta di estendere le proprietà di continuità, derivabilità e integrabilità alla funzione limite (con relativo passaggio a limite sotto il segno di integrale e derivata).
Analisi Matematica II: Successioni di funzioni – Lezione 2

Guarda il video
(Pubblicazione 30.07.2023)
Nel video vengono risolti due esercizi riguardanti la convergenza puntuale e la convergenza uniforme di due successioni di funzioni. Per una delle due successioni di funzioni viene anche calcolato l’integrale utilizzando il teorema di passaggio al limite sotto il segno di integrale.
Analisi Matematica II: Successioni di funzioni – Lezione 3

Guarda il video
(Pubblicazione 05.08.2024)
Nel video vengono risolti due esercizi riguardanti la convergenza puntuale e la convergenza uniforme di due successioni di funzioni. Per una delle due successioni di funzioni viene anche calcolato l’integrale utilizzando il teorema di passaggio al limite sotto il segno di integrale.
AM II: Serie di funzioni – Convergenza puntuale – Lezione 1

Guarda il video
(Pubblicazione 20.12.2024)
Nel video vengono introdotte le serie di funzioni e, in particolare, viene trattata la convergenza puntuale.
Dopo una breve introduzione, vengono svolti tre esempi in cui è richiesto di verificare se la serie di funzioni converge puntualmente determinandone l’eventuale insieme di convergenza puntuale.
AM II: Serie di funzioni – Convergenza assoluta e uniforme – Lezione 2

Guarda il video
(Pubblicazione 24.02.2025)
Nel video vengono introdotte la convergenza assoluta e la convergenza uniforme.
Dopo averne data la definizione vengono svolti esercizi in cui è richiesto di dimostrare, utilizzando la definizione, che una data serie di funzioni sia o meno uniformemente convergente su un certo intervallo.
AM II: Serie di funzioni – Il criterio di Weierstrass – Lezione 3

Guarda il video
(Pubblicazione 25.02.2025)
Nel video viene introdotto il criterio di Weierstrass per lo studio della convergenza uniforme di una serie di funzioni.
Successivamente vengono svolti vari esercizi di esempio per mostrarne l’applicazione.