Data la curva
![]()
stabilire se è chiusa, semplice e regolare.
1) Chiusura

Poichè la curva è chiusa.
2) Semplicità
Dobbiamo capire se “un punto materiale che si muova con legge passa più volte per uno stesso punto”.
Studiamo separatamente il moto del punto materiale lungo l’asse e lungo l’asse
.
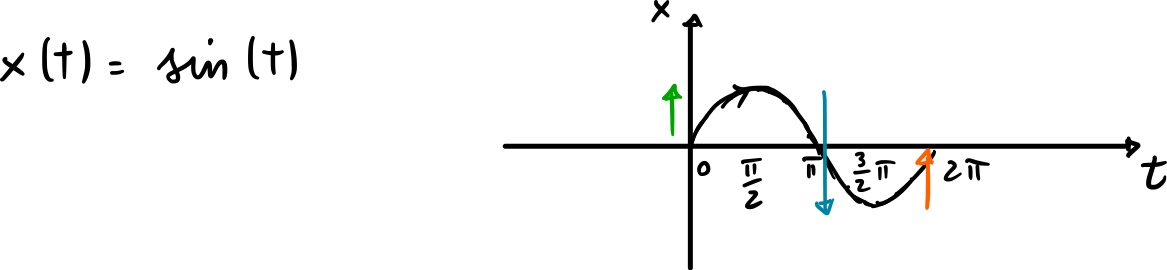
La cresce tra 0 e
, poi decresce tra
e
, infine cresce tra
e
.

La decresce tra 0 e
, cresce tra
e
, decresce tra
e
infine cresce tra
e
.
Combinando il moti, nel piano si ha:
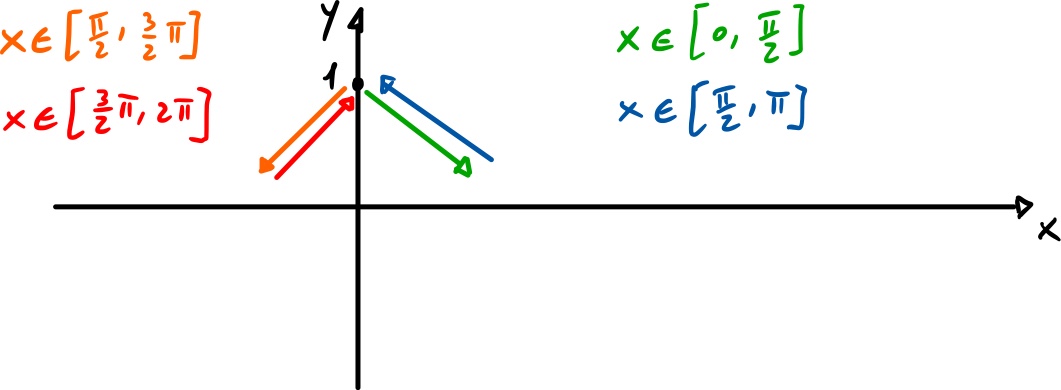
Si vede che il punto materiale passa più volte negli stessi punti, ad esempio:
.
La curva quindi non è semplice.
3) Regolarità
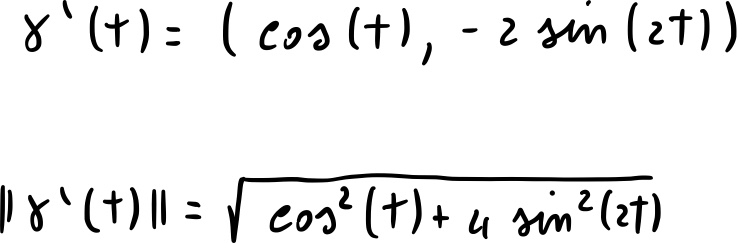
Vediamo se esistono punti tali che .
Si vede che per si ha:
![]()
Poichè esiste almeno un punto in tale che
, la curva non è regolare.
Osservazione
Si noti che i punti di non regolarità sono quelli di inversione (“brusca”) del moto (in corrispondenza di tali punti il sostegno della curva presenta delle cuspidi).
Il sostegno della curva che abbiamo studiato è dato da:

Per tanti altri esercizi svolti seguitemi sul mio profilo Instagram: @gquadroblogesercizi