Studiando alcuni argomenti di matematica, come ad esempio i campi vettoriali, campita di dover studiare alcune proprietà degli insiemi.
In questo articolo ci soffermeremo sulla connessione (semplice o meno) di un insieme.
Insiemi connessi (per archi)
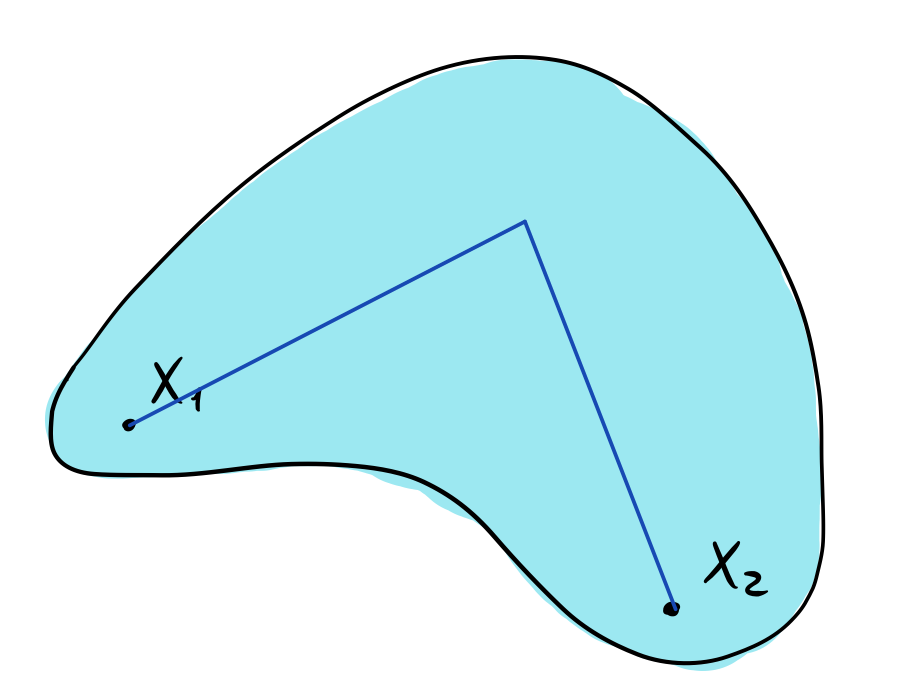
Un insieme aperto 
si dice connesso (per archi) se presi in 
due punti qualsiasi 
e 
esiste una poligonale che li congiunge interamente contenuta in .
Esempi
- In
gli unici insiemi connessi sono gli intervalli aperti - In
ogni insieme aperto convesso è anche connesso - L’insieme
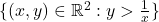non è connesso:
Insiemi semplicemente connessi
Un insieme aperto 
si dice semplicemente connesso se il sostegno 
di ogni arco contenuto in 
può essere deformato con continuità fino a diventare un punto, rimanendo sempre all’interno dell’insieme .
Una definizione equivalente può essere:
un insieme si dice semplicemente connesso se ogni curva chiusa contenuta al suo interno può essere deformata con continuità fino a diventare un punto.
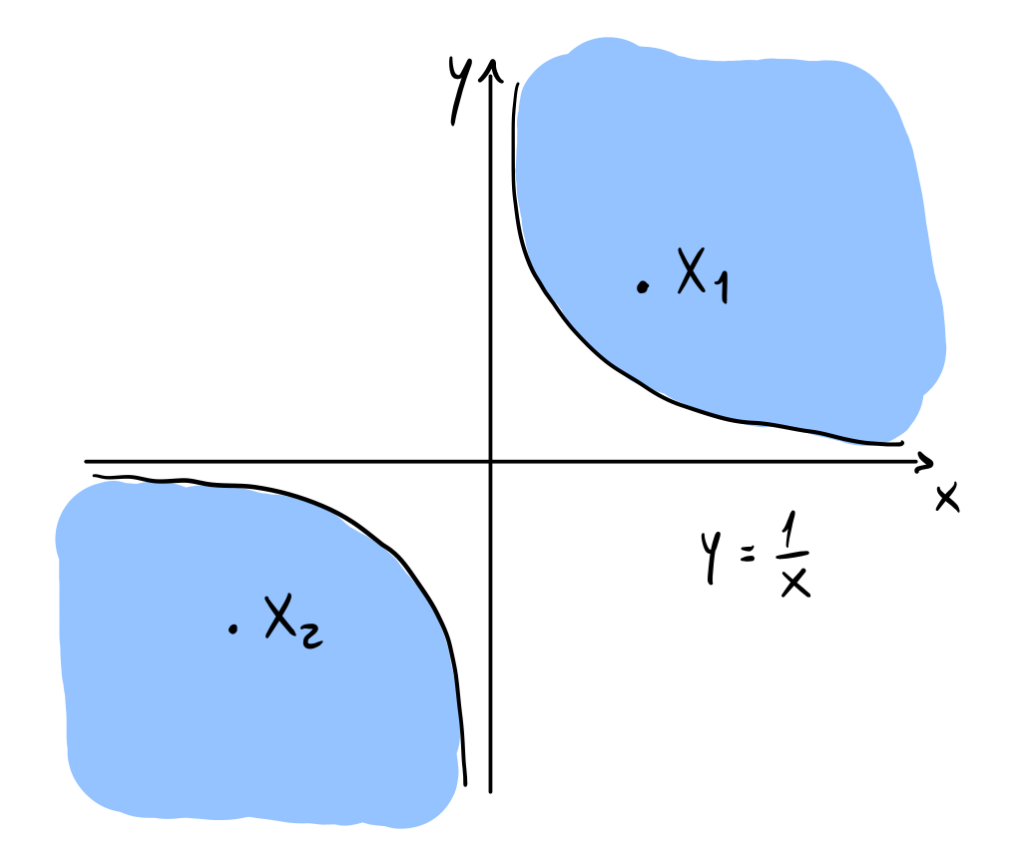
Ad esempio, nell’immagine che segue, si ha che 
è un insieme semplicemente connesso in quanto ogni curva chiusa al suo interno può essere deformata fino a diventare un punto (analogamente a ciò che avviene stringendo un cappio); l’insieme 
non è semplicemente connesso perché una curva chiusa che circonda il buco può essere “ristretta” fino al bordo del buco e non oltre (non riesce a diventare un punto).
Ancora potremmo usare la seguente definizione:
un insieme si dice semplicemente connesso se ogni curva chiusa 
contenuta al suo interno è omotopa a un punto.
La definizione precedente deriva dal fatto che chiamiamo omotopia la funzione che permette di passare dalla curva iniziale al punto.
Supponiamo, infatti, di avere una famiglia di curve chiuse 
con 
e che la curva appartenga a tale famiglia in modo che valga 
. Assunto che:
- la funzione
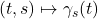definita da ![\gamma_s : I \times [0,1] \to \mathbb{R}^n](https://www.gquadroblog.com/wp-content/ql-cache/quicklatex.com-4d9d2b7c2a51ac27143939d8955b11a7_l3.png "Rendered by QuickLaTeX.com")
è continua (tale funzione è quella che associa l’s-esimo elemento della famiglia alla curva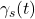 
) - il sostegno
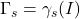di ogni curva è contenuto in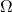 
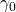è costante (ossia il suo sostegno è un punto)
l’omotopia è proprio la funzione e la curva viene detta essere omotopa a un punto.
Osservazione 1
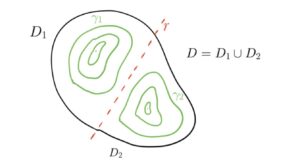
Un insieme semplicemente connesso privato di una retta continua ad essere semplicemente connesso in quanto può essere considerato unione di due insiemi semplicemente connessi.
