Il teorema dei lavori virtuali nella sua duplice formulazione

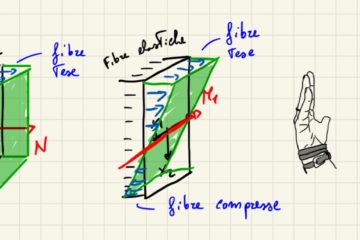
Spostamenti Virtuali

Consideriamo un sistema di forze e tensioni equilibrate:

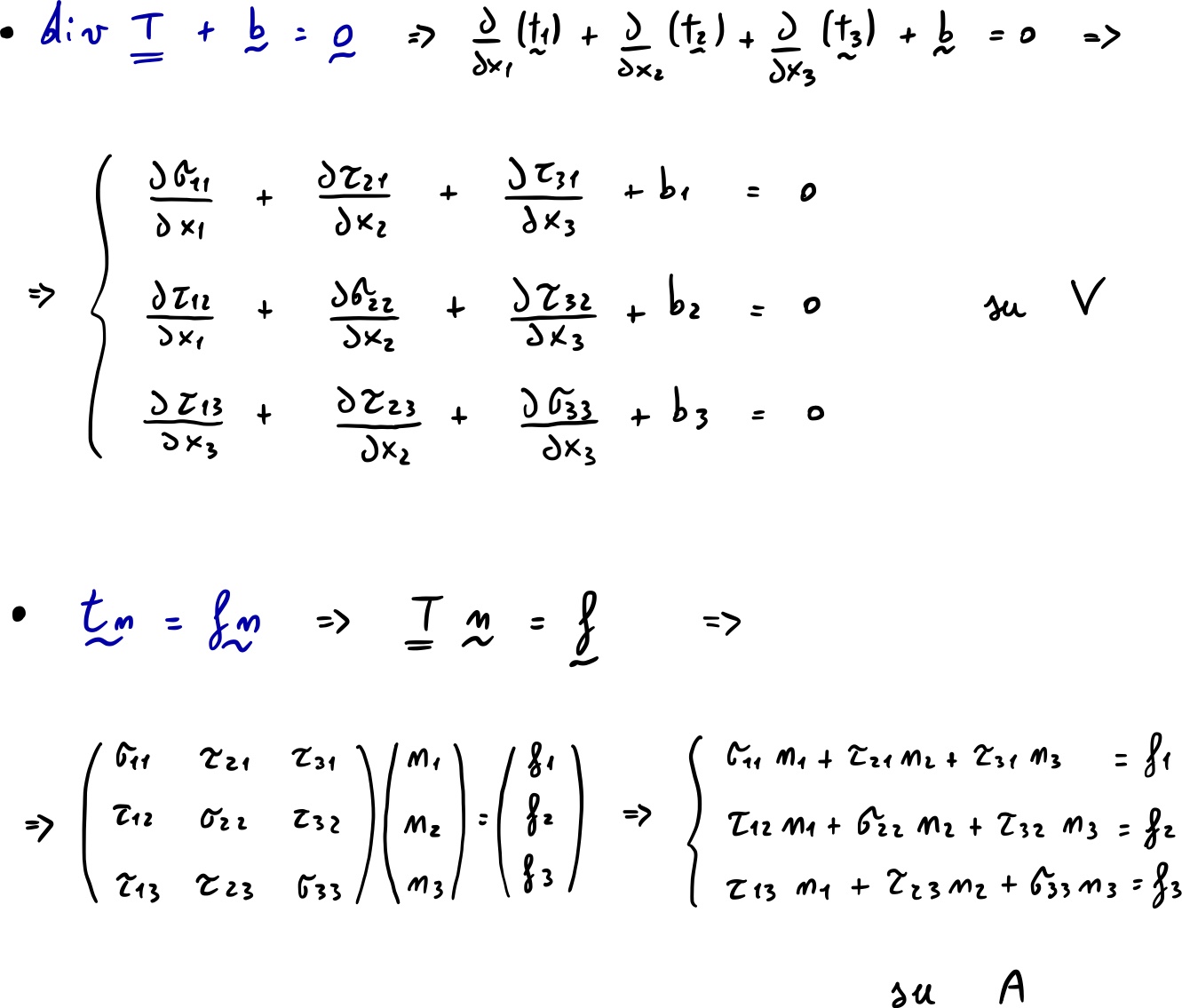
Consideriamo un sistema di spostamenti e deformazioni virtuali congruenti:

Eguagliando termine a termine le componenti delle due matrici (e ricordando che la matrice E è simmetrica) si ha:

Definito il lavoro virtuale esterno:

e il lavoro virtuale interno:

si ha che:

Forze virtuali

Consideriamo un sistema di spostamenti e deformazioni congruenti:

Consideriamo un sistema di forze e tensioni virtuali :

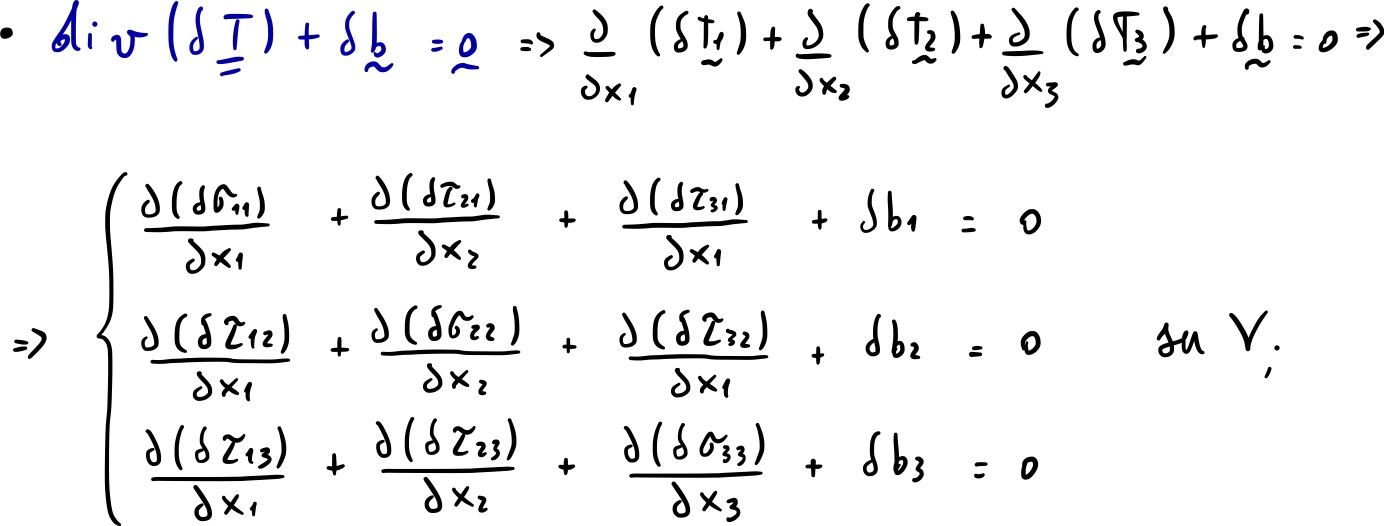
Definito il lavoro virtuale complementare esterno:

e il lavoro virtuale complementare interno:

si ha:

Per tanti altri esercizi svolti seguitemi sul mio profilo Instagram: @gquadroblogesercizi