Sistema lineare – G-quadroblog

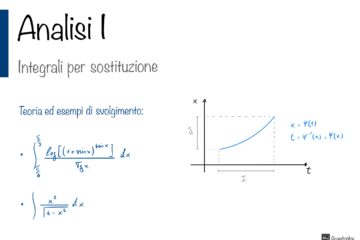
Studiare le soluzioni del seguente sistema lineare al variare del parametro $k$ :

Per studiare il comportamento del sistema mi avvalgo del teorema di Rouché – Capelli. Studio quindi il rango della matrice dei coefficienti e della matrice completa.

La matrice dei coefficienti è data da:

Per determinarne il rango analizziamo le sottomatrici $2 \times 2$ :

Quindi:

Studiamo la matrice completa:

Determiniamo è il rango studiando le varie sottomatrici:

Si vede che per $k \neq 3 \ \rightarrow \ Rg(A|b)=3$ .

Per $k=3$ :

Le colonne della matrice sono “linearmente dipendenti” e quindi il $Rg(A|b)=1$ .

Dunque:

Mettendo insieme i risultati ottenuti:

per $k \neq 3 \ \rightarrow \ Rg(A)=2 \neq 3 = Rg(A|b) \ \rightarrow$ il sistema è incompatibile;

per $k = 3 \ \rightarrow \ Rg(A)=1 = Rg(A|b) \ \rightarrow$ il sistema è compatibile e possiede $\infty ^{2-1}$ soluzioni, cioè $\infty ^{1}$ soluzioni.

Ciò vuol dire che i punti soluzione del sistema formano una retta (la retta ha dimensione $\infty$ ).

Significato geometrico dell’esercizio

La prima equazione del sistema rappresenta la retta $y=\frac{2}{3}x +\frac{1}{3}$ .

La seconda equazione rappresenta un fascio di rette di centro $\biggr (-\frac{1}{2}, \ 0 \biggl )$ .

La terza equazione rappresenta un fascio di rette improprio di rette parallele alla retta $y=\frac{2}{3}x$ .

Per $k=3$ le tre equazioni coincidono e dunque rappresentano la stessa retta, i cui punti risolvono il sistema.

Per $k\neq 3$ le tre rette non hanno alcun punto in comune.

Categorie: Algebra lineare e geometria analiticaEsercizi di Analisi IEsercizi sui sistemi lineari

Tag: algebraesercizi svoltigeometria analiticamatematicaRipetizioniripetizioni on lineRipetizioni Romaripetizioni Skypestudentitutor on lineuniversità