Introduzione.
Insiemi limitati: estremo superiore ed inferiore, massimo e minimo.
Il concetto di funzione: dominio, codominio, immagine, grafico, biiettività. Le funzioni di variabile reale: funzioni limitate, simmetriche, monotone, periodiche. Operazioni sui grafici. Funzioni elementari (segno, parte intera, valore assoluto, potenze reali, esponenziali, logaritmi, funzioni trigonometriche, funzioni iperboliche).
Simbolo di sommatoria: somma della progressione geometrica. Fattoriale e coefficiente binomiale.
Numeri complessi.
Forma algebrica, trigonometrica ed esponenziale dei numeri complessi. Le 4 operazioni elementari. Potenze, radici, polinomi, esponenziali; equazioni in campo complesso.
Successioni e serie numeriche.
Il concetto di limite e le sue proprietà: unicità del limite, successioni limitate. Algebra dei limiti.
Infinitesimi ed infiniti. Teoremi di confronto (confronto, permanenza del segno I e II, carabinieri e conseguenze).
Successioni monotone: teorema di regolarità. Alcuni limiti notevoli. Il concetto di serie e le sue proprietà. Condizione necessaria per la convergenza di una serie. Serie a termini non negativi e teorema di regolarità. Criteri di convergenza per le serie a termini non negativi: criterio del confronto e del confronto asintotico, del rapporto, della radice. Serie a termini di segno qualunque: assoluta convergenza e criterio di Leibniz. Studio della serie geometrica, della serie di Mengoli, delle serie telescopiche, della serie armonica generalizzata e della serie di Abel.
Limiti e continuità delle funzioni di una variabile.
La nozione di limite e sue proprietà. Definizione di continuità: operazioni elementari e funzioni continue. Punti di discontinuità. Asintoti. Teorema degli zeri, Teorema di Weierstrass, Teorema dei valori intermedi. Funzioni monotone su intervalli. Funzioni composte e funzioni inverse. Funzioni trigonometriche inverse (arcocoseno, arcoseno, arcotangente). Calcolo differenziale per funzioni di una variabile. Il concetto di derivata e sue proprietà: retta tangente e approssimazione lineare. La definizione di “o” piccolo.
Derivate elementari. Derivata della funzione composta e della funzione inversa. Punti di non derivabilità. Caratterizzazione delle funzioni costanti su intervalli. Estremi locali e Teorema di Fermat. Teorema di Lagrange e Criterio di monotonia. Derivate di ordine superiore: concavità e convessità. Studio del grafico di una funzione di variabile reale. Teorema di de L’Hopital. Formula di Taylor (cenni alle serie di Taylor).
Teoria dell’integrazione I.
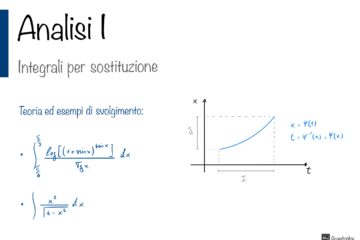
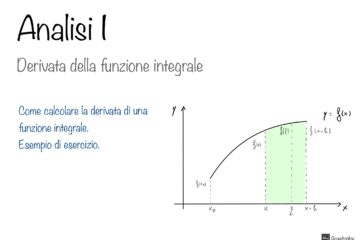
Definizione dell’integrale di Riemann e sue proprietà. Significato geometrico. Teorema della media. Classi di funzioni integrabili e proprietà dell’integrale. Integrale indefinito: funzioni primitive e loro caratterizzazione. Il 1° Teorema fondamentale del calcolo integrale. Alcuni metodi di integrazione (integrali elementari, decomposizione in somma, per parti, per sostituzione, funzioni razionali, funzioni trigonometriche, alcune funzioni irrazionali). La funzione integrale e il 2° Teorema fondamentale del calcolo integrale (Teorema di Torricelli). Integrali di funzioni discontinue. Integrali impropri: criteri di convergenza al finito e all’infinito.
Algebra dei vettori.
Vettori del piano e dello spazio: definizione e proprietà. Somma di due vettori del piano o dello spazio e prodotto per uno scalare: definizione e loro interpretazione geometrica e fisica. Somma di vettori e prodotto di un vettore per uno scalare. Combinazione lineare tra vettori. Dipendenza ed indipendenza lineare. Norma di un vettore: definizione e proprietà. Versori. Prodotto scalare: definizione geometrica e proprietà. Caratterizzazione del prodotto scalare in termini delle componenti dei vettori. Ortogonalità. Prodotto vettoriale: definizione geometrica e sue proprietà.
Algebra lineare.
Equazioni lineari. Sistemi lineari. Equivalenza di sistemi, matrici, equivalenza per righe di matrici. Matrici ridotte, matrici triangolari. Rango di una matrice. Compatibilità e incompatibilità di un sistema lineare. Teorema di Rouché-Capelli. Sistemi omogenei. Dimensione delle soluzioni di un sistema omogeneo. Discussione di sistemi dipendenti da parametri. Determinante di una matrice quadrata. Minori di una matrice. Definizione di rango usando i determinanti.
Rango di una matrice e dipendenza e indipendenza lineare dei vettori righe e dei vettori colonna. Base e dimensione di uno spazio vettoriale. Cambiamenti di riferimento. Cambiamenti di coordinate nel piano e nello spazio. Cambiamenti di coordinate ortonormali (rotazioni e traslazioni). Prodotto tra matrici (righe per colonne). Notazioni matriciali per i cambiamenti di riferimento. Matrice del cambiamento di riferimento. Matrice trasposta, matrice identità e matrice inversa.Trasformazioni lineari (esempi: omotetie, rotazioni, trasformazioni diagonali). Autovalori e autovettori.
Geometria analitica del piano e dello spazio
Equazione cartesiana ed equazioni parametriche di una retta del piano. Vettore direzione di una retta: coefficiente angolare e parametri direttori. Condizioni di parallelismo e perpendicolarità tra rette del piano. Individuazione dell’angolo tra due rette attraverso il prodotto scalare. Fascio di rette per un punto.
Coniche: circonferenza, ellisse, iperbole e parabola.
Equazione parametriche di una retta dello spazio. Equazione cartesiana di un piano, fasci di piani ed equazioni cartesiane della retta nello spazio. Condizioni di parallelismo e perpendicolarità tra piani e rette.